随机过程定义
定义 设是概率空间, T是给定的参数集, 如果对于任意
, 都有一定义在
上的随机变量
与之对应, 则称随机变量族
. 简记为
或
或
.
1. 关于概率空间
随机实验是指其结果不能事先准确地预言, 并且在相同条件下可以重复进行的那种实验.
随机实验的所有可能结果组成的集合称为这个试验的样本空间或基本事件空间, 记为,
中的元素
称为样本点或基本事件.
样本空间的子集称为随机事件, 简称事件. 称事件
发生, 当且仅当
中的一个样本点出现. 样本空间
也是一个事件, 称必然事件, 空集
称为不可能事件.
定义 1.1 设是样本空间,
是由
的一些子集构成的集类(族), 如果它满足:
则称
定义 1.2 设
称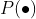 为
为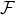 上的概率,
上的概率,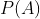 为事件
为事件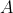 的概率, 并且称三元总体
的概率, 并且称三元总体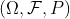 为概率空间.
为概率空间.
用集合来定义概率空间的好处是可以以集合的观点来思考概率问题,尤其是借助文氏图,可以使问题更加直观。
2. 对随机过程的理解
数学上, 随机过程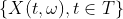 是定义在
是定义在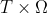 上的二元函数. 当
上的二元函数. 当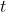 固定时,
固定时, 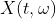 是
是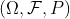 上的随机变量
上的随机变量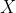 ; 当
; 当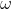 固定时,
固定时,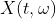 是定义在
是定义在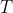 上的普通函数, 称为随机变量
上的普通函数, 称为随机变量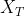 上的一个样本函数或轨道(或实现).
上的一个样本函数或轨道(或实现).
物理上, 随机过程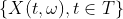 也是一个系统. 当
也是一个系统. 当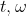 都固定时,
都固定时, 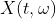 为一个实数, 表示系统在
为一个实数, 表示系统在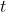 时刻所处的状态.
时刻所处的状态.
用集合来定义概率空间的好处是可以以集合的观点来思考概率问题,尤其是借助文氏图,可以使问题更加直观。
2. 对随机过程的理解
数学上, 随机过程
物理上, 随机过程